Fluid Systems

Fluid systems are central to engineering because they describe how pressure, flow, and energy interact in liquids and gases. These principles are widely applied in hydraulics, pneumatics, aerodynamics, and process systems, making them essential for system modeling.

Pascal’s Law

At the foundation lies the concept of pressure, which is the force applied per unit area:

P = \frac{F}{A}

(Here, P is pressure, F is force, and A is area.)

density

Mass in a fluid can be related to density and volume:

M = \rho V

(Here, M is mass, ρ is density, and V is volume.)

governing equation

\dot{m} = w_in - w_out

mass flow rate

When analyzing moving fluids, the mass flow rate which is amount of mass passing through a point per unit time is given by:

w = \frac{1}{R} (P_1-P_a)^{\frac{1}{\alpha}}

(where 1 < alpha < 2, 1 on long tube like Re < 100, and 2 on short tube like Re > 10^5)

or,

w = \frac{\Delta m}{\Delta t} = \rho A v

(Here, ṁ is mass flow rate, A is cross-sectional area, and v is velocity.)

Pressure Measurement

Fluid systems also distinguish between absolute and gauge pressure. Absolute pressure includes atmospheric pressure, while gauge pressure measures relative to it:

P_{absolute} = P_{gauge} + P_{atm}

(Here, P_atm is atmospheric pressure which is about 101.325kPa)

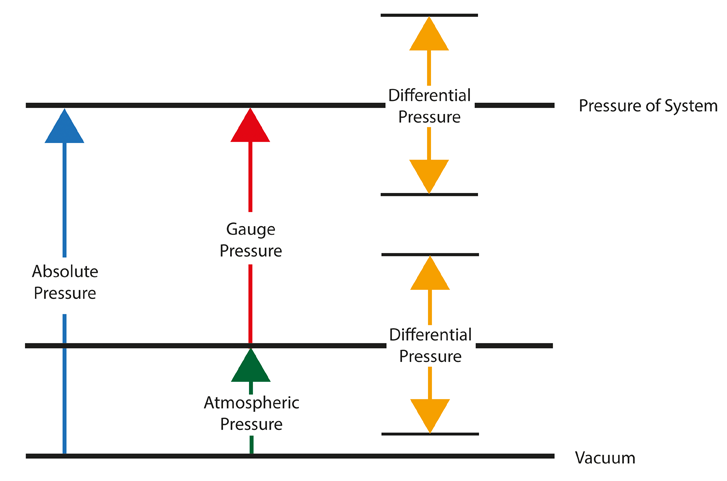Super wide Figure 1 (from https://energyeducation.ca/encyclopedia/Gauge_pressure)

However, differential pressure (DP or ∆P) is the difference in pressure between two points of pressure. To generate a reading one of the two pressures is either higher or lower than the other. If they are the same then no pressure reading will be generated.

Buoyancy Force

Another important principle in fluid systems is buoyancy. An object submerged in a fluid experiences an upward buoyant force equal to the weight of the displaced fluid:

F_b = \rho_f g V

(Here, F_b is buoyant force, ρ_f is fluid density, g is gravitational acceleration, and V is displaced volume.)

Bernoulli’s Equation

Energy conservation in a flowing fluid is governed by Bernoulli’s principle, which states that the sum of pressure, kinetic energy per unit volume, and potential energy per unit volume remains constant:

P + \frac{1}{2} \rho v^2 + \rho g h = \text{constant}

(Here, g is gravitational acceleration and h is elevation.)
This shows the trade-off: slow velocity corresponds to higher pressure, while fast velocity corresponds to lower pressure.

The work done by pressure forces translates into kinetic energy:

W = \Delta Kinetic Energy = Kinetic Energy_{final} - Kinetic Energy_{initial}

So,

W + K E_I = K E_F

Which is,

F_{net} d + \frac{1}{2} m v_1^2 = \frac{1}{2} m v_2^2

(Here, W is work, m is mass, v₁, v₂ are velocities, and F_net is net force which is the the change in work done on the fluid, which comes from pressure differences, changes in kinetic energy, and work done by gravity.)

Pascal’s Law describes how pressure is transmitted equally in all directions, enabling force multiplication. In a hydraulic press:

F_{net} = F_1 - F_2 = P_1 A - P_2 A

(Here, F₁, F₂ are forces and A₁, A₂ are piston areas.)

Finally,

P_1 - P_2 + \frac{1}{2} P_1 V_1^2 (+ \rho g h_1) = \frac{1}{2} P_2 V_2^2 (+ \rho g h_2)

Ultimately, fluid system modeling explains how pressure drives flow, how Bernoulli’s principle links velocity and pressure, how buoyancy arises from displaced volume, and how hydraulics provide mechanical advantage. By combining these ideas, engineers can analyze and optimize systems ranging from water distribution networks to aircraft design, ensuring both efficiency and reliability.